2^da Competencia de Clubes Cabri

Primera ronda

1^er nivel

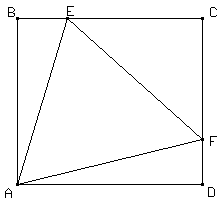
1. Construir la figura dada, en donde ABCD es un cuadrado y AEF es un triángulo equilátero.

2. Sea ABC un triángulo isósceles (AB = AC). Se traza la mediatriz m de AC y la bisectriz n del ángulo C. Si m, n y AB se cortan en un sólo punto, cuánto mide el ángulo A?

3. Sean A, B y C puntos sobre una circunferencia. Llamemos H al ortocentro del triángulo. Hallar el lugar geométrico de H al mover A sobre la circunferencia.

1^er nivel

4. Dados 3 puntos A, B y C, construir el trapecio isósceles ABCD donde AB = CD y BC es paralelo a AD (BC distinto de AD).

5. Sean A, B y C puntos sobre una circunferencia. Llamemos G al baricentro del triángulo. Hallar el lugar geométrico de G al mover A sobre la circunferencia.

6. Dado un triángulo ABC, sean D, E y F los puntos medios de los lados BC, CA y AB respectivamente. Por D se trazan las rectas M₁ y M₂ perpendiculares a AB y AC respectivamente. Por E se trazan las rectas M₃ y M₄ perpendiculares a BC y AB respectivamente. Por F se trazan las rectas M₅ y M₆ perpendiculares a AC y BC respectivamente. Sea A´ la intersección entre M₄ y M₅. Sea B´ la intersección entre M₆ y M₁. Sea C´ la intersección entre M₂ y M₃. Demostrar que los triángulos ABC y A´B´C´ son semejantes y hallar la razón de semejanza.

[ 2da Competencia  - Ronda final ]

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar