15ta
Competencia de Clubes Cabri
Primera Ronda
22 de agosto al 4 de septiembre de 2001
Nivel A
1
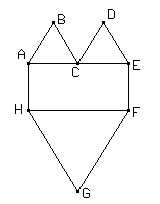
Construir la siguiente figura donde ABC, CDE y FGH son triángulos equiláteros; AEFH es un rectángulo y AC = CE = EF.

2
En la figura del problema 1, hallar la medida del segmento BG.
3
En la figura del problema 1, hallar el ángulo que forman las rectas BH y DF.
4
Sea ABCD un cuadrado, de
área 30.
Sea P un punto en el lado AB tal que 2 . AP
= PB.
Sea Q un punto en lado BC tal que BQ = QC.
Sea R un punto en lado AD tal que 2 . DR = RA.
La recta PQ corta a la recta CD en M y la
recta PR corta a la recta CD en N.
Hallar el área del triángulo MNP.
5
Dado un cuadrado ABCD, construir un triángulo isósceles de igual área y con un lado igual al lado del cuadrado.
Nivel B
6
Sea ABCD un paralelogramo con <DAB agudo. La bisectriz de < DBC corta al lado CD en Q y a la recta AD en P. Si AD = DP, hallar la medida del ángulo <DQB.
NOTA: el símbolo <DAB significa "ángulo DAB".
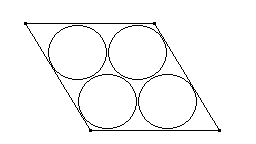
7
Construir la siguiente figura formada por 4 circunferencias de igual radio, tangentes entre sí y tangentes a los lados del paralelogramo.
8
Si en el problema anterior el radio de las circunferencias es 1cm, hallar el área del paralelogramo.
9
Dado un cuadrado ABCD, construir un triángulo isósceles PQR de igual perímetro que ABCD y tal que la base de PQR mida la mitad de los otros dos lados.
Nivel C
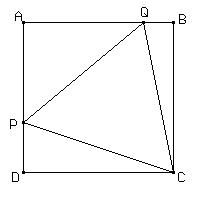
10
Construir la siguiente figura, donde ABCD es un rectángulo, PQC es equilátero y 2 PD = PA.
11
Sea ABC un triángulo isósceles, de base AB = 10cm. Sean M y N son los puntos medios de los lados AC y BC respectivamente. Sea G el punto de intersección de BM y NA.
Si el ángulo AGB es recto, hallar el área de ABC.
12
Sean A, B, C
y D cuatro puntos alineados tales que AB = BC
= CD.
Sea P un punto del plano tal que 2 <APB = <BPC
= 2 <CPD.
Hallar la medida del ángulo <APB.
13
Sean S y R dos circunferencias de centro O1 y O2 respectivamente. Sea P un punto en S. Se traza por P una paralela a O1O2, que corta a R en A y B. Las rectas PO1 y AO2 se cortan en un punto E.
Hallar el lugar geométrico de E al mover P sobre S.
15ta
Competencia de Clubes Cabri
Primera Ronda
Carátula
Nombre del Club: ..............................................................................
Nivel: A B
C
(Tachar lo que no corresponda)
Miembros que participan de esta ronda en el nivel indicado.
| Nombre | Apellido |
Reglamento
Personalmente o por carta,
Clubes Cabri
Fundación Olimpíada Matemática Argentina
Santa Fe 3312 9º piso
Capital Federal
Por teléfono o fax, (011) 4826-6900
Por correo electrónico: cabri@oma.org.ar
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |