14ta
Competencia de Clubes Cabri
Primera Ronda
2 al 11 de mayo de 2001
| nivel A |
1
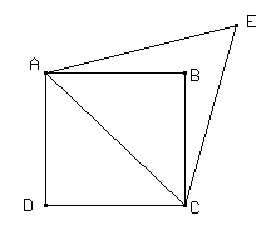
Construir la siguiente figura donde ABCD es un cuadrado y ACE es un triángulo equilátero.

2
En la figura anterior hallar la medida de los ángulos internos del triángulo ABE.
3
Sabiendo que AB = 1, hallar la longitud del segmento DE y la distancia del punto E a la recta CD.
4
Construir un cuadrado PQRS y un triángulo equilátero XYZ tales que el perímetro del cuadrado sea el doble que el perímetro del triángulo.
5
En el problema anterior: Si el cuadrado tiene área 16, ¿cuál es el área del triángulo equilátero?
| nivel B |
6
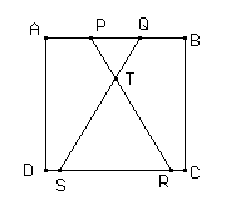
Construir la siguiente figura formada por un cuadrado y dos triángulos equiláteros, tal que la longitud del lado del triángulo más chico es la mitad de la longitud del lado más grande. Se sabe además que T está en la mediatriz de AB.
7
En la figura anterior: Si el lado cuadrado mide 2cm, ¿cuál es el área del cuadrilátero PQRS?
8
Hallar la medida de los segmentos AT, AS y AR.
9
Construir un triángulo ABC tal que BAC = 45° y BC = 2 . AB.
| nivel C |
10
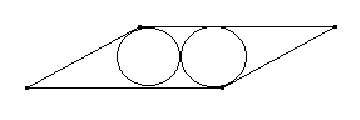
Construir la siguiente figura formada por un paralelogramo y dos circunferencia tangentes entre sí y tangentes a tres lados del paralelogramo sabiendo que el radio de las mismas mide la cuarta parte del lado menor del paralelogramo.
11
En el problema anterior, sea x la longitud del lado mayor del paralelogramo y r el radio de las circunferencias. Hallar la razón x / r.
12
Construir un triángulo ABC tal que BAC = 30° y su área sea igual a BC2 / 2.
13
Sean A, B y C tres puntos alineados, en ese orden. Sea r una recta perpendicular a AB que pasa por B y sean los puntos D y E sobre la recta r tal que:
Hallar la medida del ángulo BMN.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |