12ma
Competencia de Clubes Cabri
Segunda Ronda
17 de junio de 2000
Duración: 2.30hs
| nivel A |
1
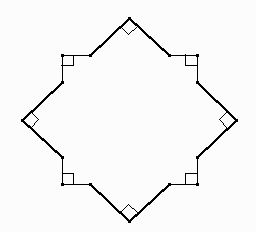
Construir la siguiente estrella donde los ángulos marcados miden 90°, los segmentos resaltados miden 2 y los demás segmentos miden 1.

2
Hallar el área de la figura del problema 1.
3
Sea ABC un triángulo equilátero de lado 4 y sea M el punto medio de AB. Sea AMP un triángulo equilátero exterior a ABC. Hallar la distancia de P a cada uno de los vértices de ABC.
4
Construir la figura del problema anterior y hallar la medida del ángulo PBC.
5
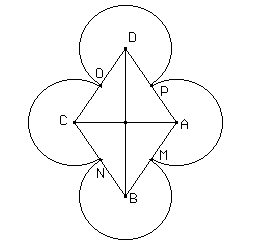
En un rombo ABCD se sabe que AC = 6 y BD = 8. Sea M el punto medio de AB, N el de BC, O el de CD y P el AD. Se trazan las circunferencias de centro D que pasa por P, la circunferencia de centro C que pasa por O, la circunferencia de centro B que pasa por N y la circunferencia de centro A que pasa por M. Así queda determinada una flor de 4 pétalos. Hallar el área y el perímetro de la flor.
| nivel B |
6
Sea ABC un triángulo. La bisectriz de A interseca a la recta perpendicular a AB por B, en el punto P. Demostrar que PB £ PC. ¿Cuándo se da la igualdad?
7
Sea ABCD un cuadrilátero tal que el área de ABD es 7 y el área de ACD es 9. Si M es punto medio de BC. Hallar el área de AMD.
8
Dados tres puntos C, M y D, construir un triángulo ABC tal que el punto C sea el vértice C del triángulo, M sea el punto medio del lado AB y D sea el pie de la perpendicular desde B a AC.
9
Sea K una circunferencia y sean A y B puntos fijos sobre ella. Sea P un punto de K distinto de A y de B. La bisectriz de PAB interseca a K en D y la bisectriz de PBA interseca a K en E. Hallar el lugar geométrico del punto medio de DE a media que P se mueve sobre K.
10
Sea ABC un triángulo acutángulo y sea P un punto sobre BC. El simétrico de P con respecto a AC es D y el simétrico de P con respecto a AB es E. La recta DE corta a AC en M y a AB en N. Demostrar que AP es bisectriz de MPN.
| nivel C |
11
Sea ABCD un cuadrilátero convexo. Sea P el simétrico de A con respecto a B; Q el simétrico de B con respecto a C; R el simétrico de C con respecto a D y S el simétrico de D con respecto a A. Hallar la razón entre el área de ABCD y la de PQRS.
12
Sea ABC un triángulo acutángulo. Sea M el pie de la altura desde A y H el pie de la altura desde B. La bisectriz de MAC interseca a BH en P y a BC en R. La bisectriz de HBC interseca a AM en S y a AC en Q. ¿Qué clase de cuadrilátero es PQRS? Justificar.
13
Sea AB segmento y sea P un punto sobre él. Sean APC y PBD triángulos equiláteros uno a cada lado del segmento AB. Hallar el lugar geométrico del punto medio de CD a medida que P se mueve sobre AB.
14
Sea ABC un triángulo y P un punto en su interior tal que PC = AB, BPC = 60° + PBA y PBC = 60°. Demostrar que BC = PA + PB.
15
Dada un circunferencia K y un punto A en su interior, distinto del centro, construir los puntos B, C y D sobre K de modo que el área de ABCD sea máxima.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |