11ma
Competencia de Clubes Cabri
Primera Ronda
1 al 8 de setiembre de 1999
| nivel A |
1
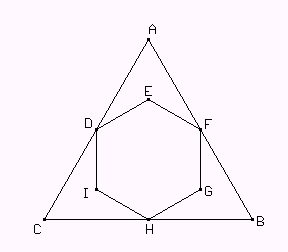
Construir la siguiente figura donde ABC es equilátero, DEFGHI es un hexágono regular y D, F y H son los puntos medios de los lados de ABC.

2
En la figura anterior hallar la razón entre las áreas de ABC y de DEFGHI.
3
Construir un rectángulo ABCD sabiendo que 50/3 del área de ABCD es igual al área del cuadrado de lado igual al perímetro de ABCD.
4
Sean a y b dos rectas. Dados los ángulos marcados, hallar el ángulo que forman a y b.
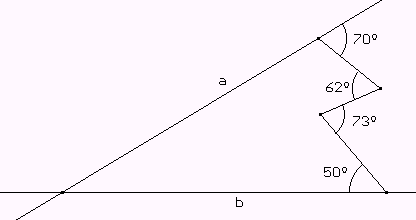
NO VALE MEDIR.
5
Sea ABCD un rectángulo tal que AB = 2 y BC = 5. Sea P un punto interior al rectángulo de modo que CPD = 90° y CP = DP. Hallar la longitud de PA.
| nivel B |
6
Construir el hexágono ABCDEF con todos sus ángulos de 120°, tal que FGCH sea un cuadrado y de modo que BC = CD.

7
Construir un triángulo ABC sabiendo que BAC = 60° y que si I es la intersección de las bisectrices de ABC entonces CIA = 135°
8
a) Dado un cuadrado ABCD de lado 1 construir un punto P tal que CPD = 30°, CP = DP y tal que P esté del mismo lado que A con respecto a CD.
b) Hallar la medida de AP.
9
Dados dos paralelogramos disjuntos trazar una recta tal que el área de las figuras que quedan a ambos lados de la recta sean iguales.
10
Sea ABCD un trapecio con AB // CD (con AD y BC no paralelos). Sea P un punto en BC y sea K en la recta CD tal que PK // AD. Demostrar que el área de ADK es la mitad del área de ABCD sí y solo sí P es el punto medio de BC.
| nivel C |
11
Sea ABC un triángulo rectángulo en B tal que AB = BC = 1. Sea D el simétrico de A con respecto a B, E el simétrico de B con respecto a C y F el simétrico de C con respecto a A. Hallar la distancia de F a la recta DE.
12
En una circunferencia de centro P, AB es un diámetro y AC es otra cuerda cualquiera. Una secante que pasa por P y es paralela a AC interseca en D a la tangente en C. Demuestre que DB es tangente a la circunferencia.
13
Dado un triángulo ABC cualquiera encontrar los puntos D y E en AC y AB respectivamente tal que si F es la intersección de BD y CF entonces: área(EFB) = área(BCF) = 2 área(CDF)
14
Sea ABCD un cuadrado de lado 5. Sea P un punto en su interior tal que PA = 3 y PB = 4. Hallar las longitudes de PC y de PD.
15
Construir un triángulo ABC tal que BAC = 30° y de modo que si M es el punto medio de BC entonces BC = AM.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |