10^ma Competencia de Clubes Cabri
Ronda final

26 de junio de 1999

Duración: 2.30hs

1

1. Construir la siguiente figura donde ABCD, AEHI y BEFG son cuadrados del mismo tamaño.

2. Hallar la medida del ángulo BDF.

2

Dada una circunferencia S, un punto A sobre S y un punto M en el interior de S, construir un triángulo ABC tal que los puntos B y C también pertenezcan a S y M sea el punto medio del lado BC.

3

En un triángulo ABC, D es el punto medio de AB y E es el punto medio de AC. Las rectas BE y CD se cortan en el punto F. Si el área del triángulo ADE es de 7 cm², ¿cuánto vale la diferencia entre el área del triángulo BCF y el área del triángulo DEF?

4

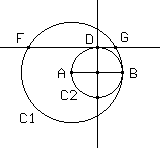
Dado un segmento AB se trazan la circunferencia C₁ de centro A que pasa por B; y la circunferencia C₂ de diámetro AB. La mediatriz de AB corta a C₂ en D. La recta paralela a AB por D corta a la circunferencia C₁ en F y G.

1. Calcular la medida del ángulo FAG.
2. Calcular la medida del ángulo AFB.

5

Construir el triángulo ABC dados: N, el punto medio de AB, el punto medio de AC y un punto P en BC tal que 2PB = PC.

6

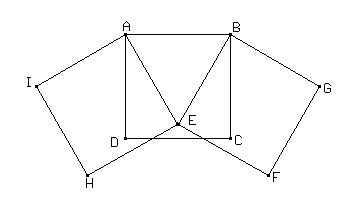
Sea ABCD un cuadrado de lado 1. Sea ACF un triángulo equilátero con D en su interior, y sea CDE un triángulo equilátero exterior a ABCD. Hallar la longitud de FE.

7

Se tienen 4 puntos alineados A, B, C y D, en ese orden. Sea C₁ una circunferencia que pasa por A y C, y sea C₂ una circunferencia que pasa por B y D. Sean E y F los puntos de intersección de C₁ y C₂. Sea M la intersección de las rectas AE y FB; sea N la intersección de las rectas DE y FC. Demostrar que MN // AD.

8

Sea ABCDEF un hexágono convexo tal que si una diagonal lo divide en 2 cuadriláteros, éstos tienen igual área. Demostrar que ACE y BDF son semejantes.

9

Dado un triángulo ABC, trazar rectas r, p y q (distintas a los lados AB, BC y AC) que pasen por A, B y C respectivamente de modo que el área del triángulo ABC sea 8 veces el área del triángulo formado por las rectas r, p y q.

10

Sea C una circunferencia y sean A y B puntos sobre C. Hallar el lugar geométrico de los puntos P tales que, si D y E son los puntos de intersección de C con las bisectrices de PAB y PBA, entonces D, E y P están alineados.

11

Sea ABCDEF un hexágono que tiene las siguientes propiedades:

• La suma de los ángulos A, C y E es 360°.
• Los lados opuestos del hexágono son iguales.

Demostrar que las áreas de ACE y BDF son iguales.

12

Sea ABCD un trapecio (con AB // CD) tal que existe un punto interior P que cumple con las siguientes condiciones:

• BPC = 60°
• PC . AB = PB . CD
• PC = PD

Hallar la medida del ángulo PÂB.

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar