Clase 3
Introducción al Caos II
Esperamos tus mails en caos@oma.org.ar.
Clase 3
Introducción al Caos II
Esperamos tus mails en caos@oma.org.ar.
Bienvenido a Caos, el curso de Omanet dedicado a los fractales y el caos. En la segunda clase, analizamos algunos algoritmos iterativos muy simples. Vamos a ver ahora unos algoritmos un poco más avanzados, que nos van a permitir asomarnos a la teoría del caos.
Antes de eso, queremos hacer una aclaración por un comentario que nos mandó Salvador sobre la clase 2:
Con respecto a los dos gráficos que hicimos iterando la función f(x) = 2 x, él nos preguntaba cómo podía ser que si graficábamos las dos veces la misma función, obteníamos gráficos distintos. En un caso obtuvimos un gráfico exponencial:

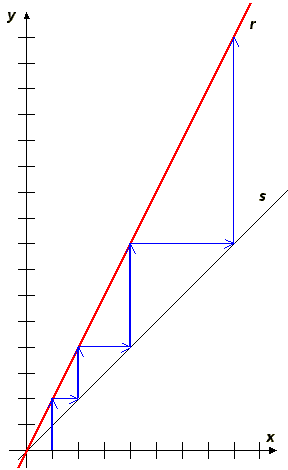
y en el otro caso una escalera (o una recta, si no miramos los puntos sobre la recta y = x):
El comentario está bien, y nos parece que mucha gente puede haber tenido la misma duda, por eso vamos a aclararlo.
La diferencia está en qué ponemos en cada eje. En los gráficos los llamamos siempre X e Y a los ejes y eso tal vez confunde.
En el primer gráfico, en el eje X está el tiempo y en el eje Y la cantidad de individuos. Es decir, para un punto t, su imagen nos dice cuántos individuos tendrá la población después de t años.
Para el segundo gráfico la interpretación no es tan clara. Tanto en el eje X como en el eje Y aparece la cantidad de individuos.
Si tomamos un punto x y miramos su imagen sobre la recta r, obtenemos cuántos individuos habrá en un año si en el año anterior había x individuos.
Pero la escalera no representa ningún movimiento real. No hay ninguna partícula moviéndose en una escalera. Es simplemente una representación del fenómeno.
Sin embargo, vamos a referirnos a este tipo de dibujos como la trayectoria por una transformación T de un punto x.
Es interesante ver para cada uno de las trayectorias que obtuvimos en la clase 2, cómo resulta el gráfico de cantidad de individuos en función del tiempo correspondiente.
Se los dejamos como ejercicio.
Otros comentarios sobre mensajes que recibimos:
Julio nos escribió:
"Quisiera saber si es posible generar fractales utilizando Matlab 5.3 o El Geómetra V.3. Además, como los podría generar."
A lo largo del curso iremos usando diversos softs para generar y estudiar los fractales y el caos. Si alguien trabajó con estos programas, o con cualquier otro, nos gustaría que nos escriba, para enriquecer el curso.
(El Geómetra es el nombre en español del Geometre Sketchpad, un soft similar al Cabri, para trabajar con geometría euclídea. El Matlab es un programa útil para distintas áreas de la matemática, y es especialmente bueno para trabajar con matrices.)
Ariel nos escribió:
"Me parece interesante la idea. Particularmente, estoy muy interesado en la teoría del caos y los fractales, y de su aplicación a finanzas. Soy estudiante de la carrera de Actuario."
Parece que sí, que los fractales tienen aplicaciones a las finanzas. Vamos a investigar sobre este tema y comentarlo en alguna clase del curso. Por supuesto, si alguien sabe sobre el tema, por favor, escriba.
Ahora sigamos con los algoritmos iterativos de la clase 2:
En la clase 2 vimos la ley de Malthus:
xk+1 = a xk
donde xk es la cantidad de individuos en el momento k y a es la tasa de crecimiento.
Esta ley no es muy realista. La población no puede crecer tan rápido, debido a los problemas de superpoblación. Cuando hay muchos individuos la tasa de crecimiento debe decrecer.
En 1976, el biólogo Roberto May formuló una nueva ley para el crecimiento de una población. Roberto supuso que la cantidad de individuos no puede pasar de un techo fijo y que en vez de una tasa de crecimiento constante a, tenemos una taza que depende de la cantidad de individuos.
Llamemos pk a la cantidad de individuos en el período k divido el techo. Por ejemplo, si el techo es de 100.000 individuos y en el período k hay 20.000 individuos, tenemos pk = 0,2. Cuando pk = 1, la cantidad de individuos ha alcanzado el techo. Por lo tanto pk se mantiene entre 0 y 1.
La ley es entonces:
pk+1 = t(pk) pk
Para elegir la función t(x), supuso que la tasa de crecimiento decrece linealmente cuando la población aumenta. Por lo tanto, t(x) = m . (1 - x). Y obtenemos
pk+1 = m . (1 - pk) pk
Observemos que para valores pequeños de pk (cercanos a cero) 1 - pk es cercano a 1 y la ecuación se parece a la ecuación original de Malthus.
Nos preguntamos qué valores puede tomar m.
Dijimos que pk está entre 0 y 1. Por lo tanto, también pk+1 está entre 0 y 1. Entonces m . (1 - pk) pk debe estar entre 0 y 1 para cualquier valor de pk entre 0 y 1.
Necesitamos entonces calcular el máximo de (1 - pk) pk para pk entre 0 y 1.
Dejamos este cálculo como ejercicio para el lector, pero damos la respuesta para poder seguir:
El máximo es 1/4. Por lo tanto m debe estar entre 0 y 4.
Vamos a estudiar como se comporta el sistema para distintos valores de m, dibujando las "trayectorias".
Empecemos con m = 1. Dibujamos la parábola y = (1 - x) x y la recta y = x.
Tomamos un punto inicial (por ejemplo, x0 = 0,7) y vamos dibujando la trayectoria.
El siguiente dibujo lo hicimos con el Derive. El libro "Aventuras Matemáticas" de Miguel de Guzmán tiene un capítulo dedicado al Caos y trae un disquete para trabajar con el Derive. Las ilustraciones que vienen están hechas con las herramientas de ese disquete.
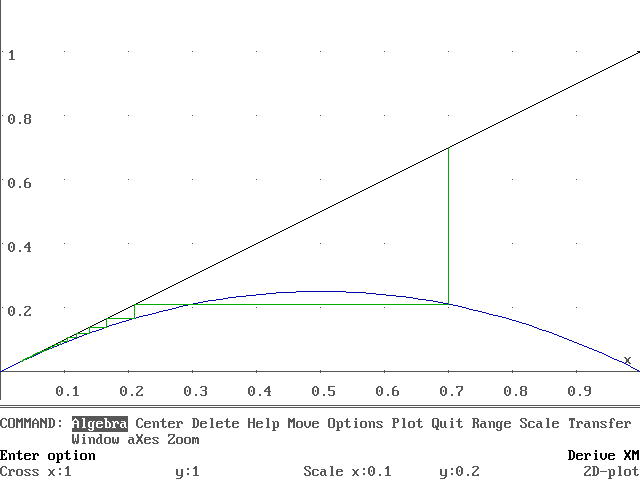
La curva violeta es la trayectoria. Como vemos, hemos obtenido también acá una escalera. La trayectoria se acerca rápidamente al origen. Esto significa que la problación tiende a desaparecer.
Esta propiedad del origen hace que lo llamemos "atractor". Si probamos empezar con otra población inicial, la trayectoria también ira rápidamente al 0.
Pero todavía no vamos a dar muchas definiciones sobre atractores, repulsores, ... Simplemente estamos viendo posibilidades.
Cambiemos la constante m por 2,8 y tomemos el punto x0 = 0,1. Obtenemos el siguiente gráfico:
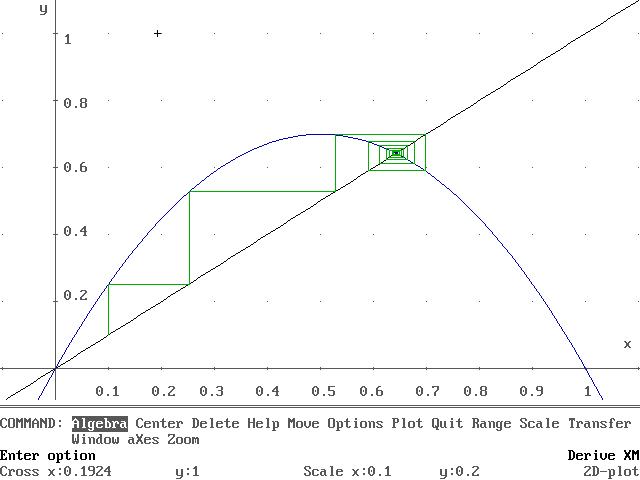
La trayectoria tambien se acerca rápidamente a un valor, que corresponde a la intersección entre la recta y = x y la parábola. Pero en este caso, lo hace siguiendo una espiral
Preguntas para el caso m=2,8:
El punto de intersección también funciona como un atractor.
Si cambiamos el valor de m por un valor más alto, la situación cambia. Ahora tomamos m = 3,5 y x0 = 0,1.
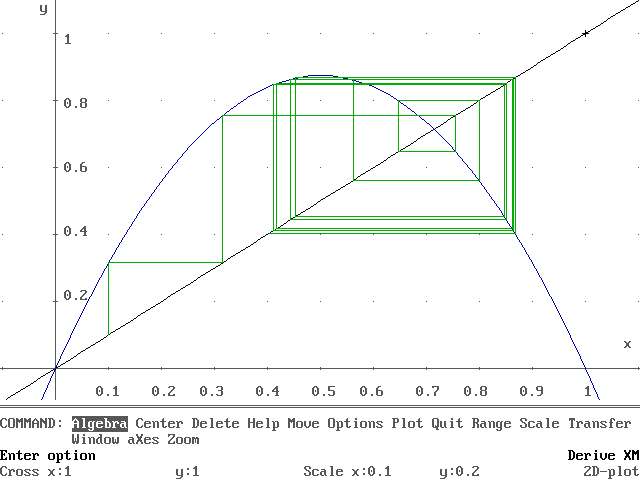
La trayectoria no se acerca al punto de intersección, sino que se aleja. Ese punto se llama entonces un "repulsor".
(En este caso, los valores de x van acercándose a dos valores distintos. La función oscila entre esos dos valores.)
Y para m mayor a 3,8 aparece un fenoméno realmente interesante. Tomemos m = 3,95 y x0 = 0,2:
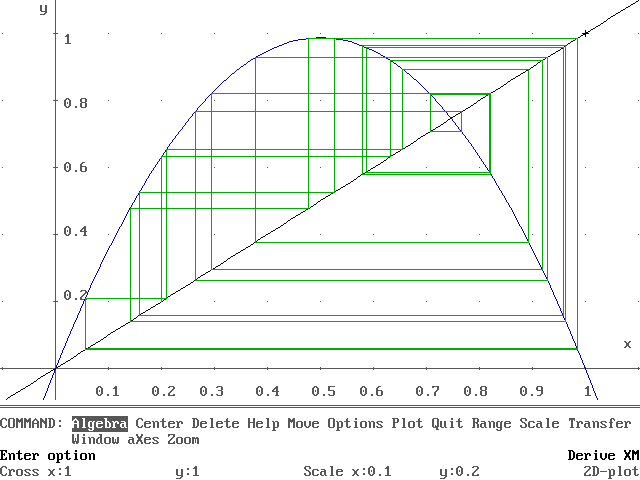
Ahora la trayectoria no muestra ningún comportamiento particular. x cambia de valor en forma totalmente irregular, aunque la función f(x) = 3,95 x (1-x) parece una función muy simple. A esto lo llamamos caos matemático.
Por fin hemos llegado a dar una mínima idea de qué es el caos. Fuimos muy rápido, porque pensamos que muchos estaban curiosos por saber qué es el caos. Pero hay mucho más para hablar sobre todo lo que vimos y muchas más cosas para ver. Lo iremos haciendo de a poco.
Así terminamos la tercer clase de Caos, el curso sobre caos y fractales de Omanet. Esperamos que te haya gustado. Dentro de dos semanas ofreceremos una nueva clase.
Mientras tanto es tu turno. Queremos que sigas las actividades y nos cuentes lo que conseguiste y las cosas que te hayan surgido. Envía tus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es caos@oma.org.ar .
También nos gustaría saber tu opinión sobre esta clase. Te pedimos que te tomes unos instantes y contestes estas preguntas. Con tu ayuda podremos hacer un curso cada vez mejor.
(Todos los campos son opcionales, pero te pedimos que nos des tu dirección de mail si nos dejás alguna pregunta o comentario.)
| OmaNet - Educación Interactiva www.oma.org.ar/omanet | omanet@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |