Clase 2
Introducción al Caos

 

Esperamos tus mails en caos@oma.org.ar.

Bienvenido a Caos, el curso de Omanet dedicado a los fractales y el caos. En la primer clase, vimos un poco sobre los fractales. Por supuesto, hay muchísimo más para ver sobre el tema. Pero vamos a pasar ahora a una pequeña introducción al Caos. En rigor, va a ser una introducción a la introducción al caos. Vamos a necesitar más clases para poder una idea precisa de la teoría del caos. Lo que veremos ahora son algunos algoritmos iterativos.

Ya comenzó la 3a Residencia en Rosario sobre Sistemás Dinámicos. Y pronto habrá una nueva residencia en Lomas de Zamora. Como una introducción al tema, el doctor Carlos Sánchez dará un curso sobre Algoritmos en Áritmetica. El curso será los días 4, 8, 12, 15 y 17 de mayo. Hay más información en www.oma.org.ar/actividades/seminario1.htm

Para acercarnos al concepto matemático de Caos empezaremos viendo ejemplos simples de los llamados Sistemas Dinámicos Discretos, que aparecen en el estudio de modelos para sistemas biológicos.

La ley de Malthus

En el siglo XIX, Malthus propuso un modelo para el crecimiento de una población de una especie. Según este modelo, la población crece siguiendo la ley

x_k+1 = a x_k

donde x_k es la cantidad de individuos en el instante k y a es la tasa de crecimiento.

Una justificación muy simple para esta fórmula es pensar que cada individuo tiene en 1 año una cantidad a de hijos y el individuo origanal muere. Si empiezan 100 indivudos, al segundo año habrá a . 100 individudos, al tercer año, habrá a . a . 100 individuos y así sucesivamente.

Consideremos una función que dada una población de x individuos, nos diga cuántos individuos habrá al año siguiente. La función que queda definida es f (x) = a x.

Si comienzan x individuos, al año habrá f (x) individuos. A los dos años, habrá f (f (x)) individuos. A los tres años habrá f (f (f (x))) individuos. Esta notación no es muy práctica. Vamos a introducir la notación f ^k(x) para indicar la aplicación de k veces la función f a x. Por ejemplo, f (f (x) ) = f ²(x). Luego de k años, habrá entonces f ^k (x) individuos.

Por favor, no confundan f ^k(x) con (f (x))^k. Lo primero denota componer f consigo mismo k veces y lo segundo es elevar el valor de f (x) a la potencia k.

Supongamos x₀ = 1, a = 2. En la siguiente tabla vemos f ^k(x₀) para algunos valores de k.

(tomaremos por convención f ⁰(x) = x)

Como vemos, según este modelo, la población crece muy rápidamente. Este es un gráfico de f ^k(x).

Aplicar f varias veces es un proceso iterativo que juega un papel muy importante en toda la teoría del caos.

Veamos otra forma de graficar este proceso iterativo.

1. Graficamos la recta f (x) = 2 x. Llamemos r a esta recta.
2. En el mismo grafico, graficamos la recta x. Llamemos s a esta recta.
3. Tomamos un punto cualquiera x₀, del eje X. Para obtener f (x₀) debemos movernos para arriba o abajo hasta la recta r.
4. Buscamos el punto f (x₀) en el eje X. Para hacer esto, nos movemos desde el punto obtenido en 3 en forma horizontal hasta la recta s. (Notar que en este punto que obtenemos, vale x = f (x₀))
5. Para obtener f (f (x₀) ), nuevamente nos movemos desde el punto en forma vertical hasta la recta r.
6. Repitiendo este proceso, obtendremos la siguiente "escalera al infinito".

7. ¿Qué pasa si tomamos como x₀ un punto negativo? Obtenemos una "escalera a -infinito".

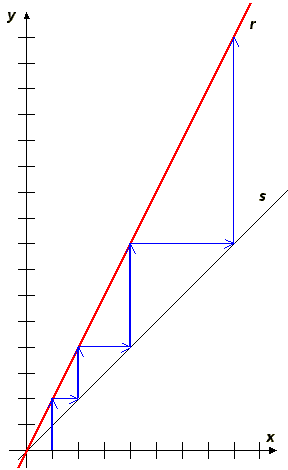
Alejándonos de la ley de Mathus, podemos pensar qué pasaría si tomamos otra recta r. Veamos por ejemplo, la recta f (x) = 1/2 x.

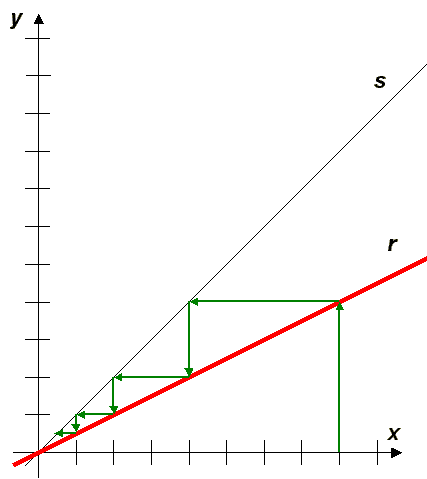
¡Obtenemos una escalera hacia adentro!

Y si tomamos la recta f (x) = - 3x/2+ 2.

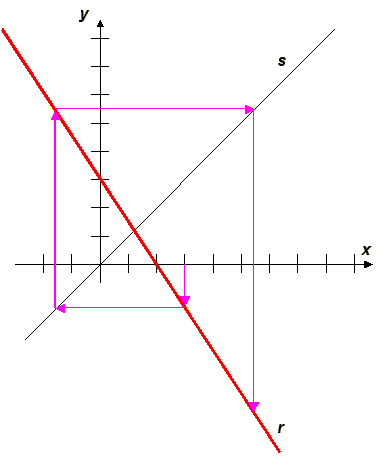
¡Ahora obtenemos una espiral!

Como vemos, hay muchas posibilidades y cosas para ver. Por ejemplo, el punto de intersección de r y s parece jugar un papel importante en todos estos gráficos. Vamos a estudiar el tema con más detalle en próximas clases.

Todavía no pudimos decir nada sobre el caos, pero estamos acercándonos. Ya vamos a llegar.

Así terminamos la primer clase de Caos, el curso sobre caos y fractales de Omanet. Esperamos que te haya gustado. Dentro de dos semanas ofreceremos una nueva clase.

Mientras tanto es tu turno. Queremos que sigas las actividades y nos cuentes lo que conseguiste y las cosas que te hayan surgido. Envía tus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es caos@oma.org.ar .

También nos gustaría saber tu opinión sobre esta clase. Te pedimos que te tomes unos instantes y contestes estas preguntas. Con tu ayuda podremos hacer un curso cada vez mejor.

Caos OmaNet   Página principal	OmaNet - Educación Interactiva    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar