. XX Olimpíada
Matemática Rioplatense
Diciembre de 2011
| Nivel A |
1. En un tablero de casillas cuadradas, Andrés y Bianca, por turnos, colocan una ficha de dominó cubriendo exactamente dos casillas vacías. Pierde el jugador que, en su turno, no puede colocar una ficha. Andrés realiza la primera jugada. Para cada uno de los siguientes tableros, decir qué jugador puede asegurarse la victoria y explicar cómo debe jugar.
• Un tablero de 3 filas por 3 columnas.
• Un tablero de 3 filas por 4 columnas.
2. Matías escribe una lista de 2010 enteros positivos. Como primer número elige un múltiplo de 2011. A partir del segundo número de la lista, la diferencia entre cada número y el anterior es 16088. Si Matías sumara los 2010 números, ¿qué valores podría tener la cifra de las unidades del resultado?
3. Para cada casilla de un tablero cuadrado, definimos sus casillas amigas como sigue:
Sobre un tablero de 2011 x 2011 hay un número entero escrito en cada casilla. La operación permitida consiste en seleccionar una casilla del tablero y para cada casilla amiga elegir entre sumar 1 ó restar 1 al número escrito en ella. Las casillas no amigas quedan sin cambios.
Si al comienzo el tablero tiene un 0 en cada casilla, ¿es posible, mediante sucesivas operaciones permitidas, obtener un tablero con un 1 en cada casilla?
Observaciones:
4. En una academia de tango hay doce personas. Para bailar cada tango, se forman parejas, pudiendo quedar algunas personas sin bailar, pero nadie baila solo. Al final de la clase, a cada persona se le preguntó cuántos tangos bailó.
Seis personas respondieron que bailaron 3 tangos, una que bailó 5 tangos, cuatro que bailaron 6 tangos y una que bailó 9.
Justificar por qué no todas las respuestas fueron correctas.
Nota: Las parejas están formadas por un hombre y una mujer.
5. Los números 1,2,…,14 están escritos en algún orden alrededor de una circunferencia. Llamamos lindo a un número si es la suma de sus dos vecinos. ¿Cuál es la mayor cantidad de números lindos que puede haber?
Dar un ejemplo para la cantidad máxima de números lindos y explicar por qué no puede haber más de ellos.
6. Se tiene un tablero de 200 x 200 y fichas de los siguientes tipos
Tipo A |
Tipo B |
Tipo C |
Tipo D |
||||||||||||||||||||
|
|
|
|
Cada ficha cubre exactamente 4 cuadraditos del tablero y está permitido girar y dar vuelta las fichas.
El tablero ha sido cubierto completamente, sin superposiciones y sin salirse del tablero, usando por lo menos una ficha de cada tipo.
Demostrar que se usó una cantidad par de fichas de tipo D.
| Nivel 1 |
1. Dado un número entero positivo N, se puede obtener un número A formado por las primeras cifras de N (de izquierda a derecha) y un número B formado por las cifras restantes en el orden en que se encuentran.
(Por ejemplo si N =1231 sólo se puede obtener: A =1, B =231; A =12, B =31; A =123, B =1.)
Decidir si para algún N es posible obtener números A y B tales que .
2. Para cada entero positivo n se define el número
.
Hallar el máximo común divisor de los 2011 números: E (1) , E (2) ,…, E (2011) .
3. Cada casilla de un tablero cuadrado de 100 x 100 se pintó de algún color, de modo que ninguna línea (fila o columna) tiene más de 4 colores distintos. ¿Cuál es el máximo número de colores que se pudo haber usado?
Explicar por qué no es posible usar más colores y dar un ejemplo de coloración que use la cantidad máxima de colores.
Segundo Día
4. Los números 1,2,…, n están escritos en algún orden alrededor de una circunferencia. Llamamos lindo a un número si es la suma de sus dos vecinos. Determinar cuál es la mayor cantidad de números lindos que puede haber en los casos:
• n =16
• n =18
En cada caso dar un ejemplo para la cantidad máxima de números lindos y explicar por qué no puede haber más de ellos.
5. Se tiene un rectángulo ABCD , con lados AB < BC . En el exterior del rectángulo se ubica el punto E tal que ABEC es un trapecio isósceles
(BE y AC son paralelas y BA=EC).
Demostrar que si el área del triángulo BEC es la cuarta parte del área del rectángulo ABCD , entonces el triángulo AED es equilátero.
6. Sea N un entero positivo. Se permite realizar las siguientes operaciones:
• Multiplicar a N por algún entero positivo.
• Si entre los dígitos de N ocurre el bloque 12345 de dígitos consecutivos, se borran estos 5 dígitos.
Demostrar que es posible, después de realizar algunas operaciones permitidas, obtener 0 a partir de cualquier N .
| Nivel 2 |
1. Los enteros positivos a , b , c , d , e , f satisfacen
.
Demostrar que 
es un número compuesto.
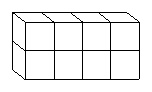
2. ¿Es posible ensamblar un cubo de 6x6x6 en los siguientes casos?
• usando solamente fichas de la forma:
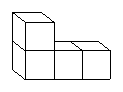
b) usando solamente fichas de la forma:
3. Sea ABCD un cuadrilátero convexo. Consideramos M un punto en el interior del segmento AB . Sean 
y 
las circunferencias circunscritas a los triángulos ACM y BDM respectivamente. Sea N el otro punto de intersección de 
y 
. Demostrar que al variar M, la recta MN pasa por un punto fijo.
4. Dados tres puntos alineados A, B, C, en ese orden, con BC = 2AB, consideramos la circunferencia G de diámetro AB . Dado P en G, sea Q el simétrico de B respecto de P, y sea R el simétrico de Q respecto de A. Por último, sea D el punto de intersección de las rectas CR y BQ. Demostrar que los triángulos BDC y QPR son congruentes.
5. Sea N mayor o igual que 59. Alrededor de una circunferencia hay escritos N números reales, no necesariamente positivos, cuya suma es 224. Cada 52 números consecutivos tienen suma mayor que 14; cada 59 números consecutivos tienen suma menor que 16. Hallar todos los valores posibles de N.
6. Un cubo Q de arista 2011 está dividido en 2011³ cubitos unitarios mediante planos paralelos a sus caras. Consideramos todos los cubos compuestos por cubitos unitarios de Q. Se deben elegir algunos de ellos de modo tal que cada cara de cada cubito unitario esté contenida en la superficie de alguno de los cubos elegidos. ¿Cuál es la menor cantidad de cubos que se deben elegir?
| Nivel 3 |
1. Dado un número natural n, una operación consiste en reemplazarlo por uno de los números 2n-1, 3n-2 ó 5n-4. Diremos que un número b es seguidor de a si b se puede obtener a partir de a mediante una sucesión de estas operaciones. Hallar todos los enteros positivos a menores que 2011 que tienen un seguidor en común con 2011.
2. Sea ABC un triángulo acutángulo y H su ortocentro. Las rectas BH y CH intersecan AC y AB en E y F respectivamente. La recta EF interseca a la recta BC en D. Sean 
la circunferencia que pasa por los puntos A , E , F , y 
la circunferencia que pasa por los puntos B , H , C. La recta AD interseca nuevamente a 
en I. Sea J el pie de la bisectriz interna de 
y M el punto medio del arco 
de 
que contiene a H . La recta MJ interseca nuevamente a 
en N. Demostrar que los triángulos EIF y CNB son semejantes.
3. Sea M un mapa formado por varias ciudades unidas unas con otras mediante vuelos. Decimos que hay una ruta entre dos ciudades si existe un vuelo sin escalas que une estas dos ciudades. Para cada ciudad a de M denotamos por 
al mapa formado por las ciudades que tienen una ruta con a y por las rutas que unen estas ciudades entre si ( a no forma parte de 
). Las ciudades de 
se dividen en dos conjuntos de modo que el número de rutas que unen ciudades de distintos conjuntos sea máximo; llamamos a este número el corte de 
. Supongamos que para todo a el corte de 
es estrictamente menor que dos tercios del número de rutas de 
. Demostrar que para cualquier coloración de las rutas de M con dos colores existen tres ciudades de M unidas por tres rutas del mismo color.
4. Consideramos 
y 
dos circunferencias que se intersecan en los puntos P y Q . Sean A , B y C puntos en la circunferencia 
y D , E y F puntos en la circunferencia 
de modo que las rectas AE y BD se intersecan en P y las rectas AF y CD se intersecan en Q. Denotemos por M y N las intersecciones de las rectas AB y DE y de las rectas AC y DF, respectivamente. Demostrar que AMDN es un paralelogramo.
5. Una forma es la unión de rectángulos cuadriculados cuyas bases son segmentos unitarios consecutivos en una recta horizontal que deja a todos los rectángulos de un mismo lado, y cuyas alturas 
satisfacen 
. Un ángulo en una forma consiste de una casilla v y de todas las casillas a la derecha de v y todas las casillas arriba de v . El tamaño de una forma o de un ángulo es el número de casillas que contienen. Hallar el máximo número de ángulos de tamaño 11 en una forma de tamaño 400.
6. Para un entero positivo n denotamos 
la suma de los divisores positivos de n y 
el número de enteros en [0, n ] que son coprimos con n . Determinar si el conjunto de los n tales que 
es un cuadrado perfecto es finito o infinito.
 Archivo de
Enunciados Página
Principal |
Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |