14^a Olimpíada Matemática Ñandú. 2005

Certamen Provincial y Metropolitano

Primer Nivel

1 Aldo y Bea escribieron cada uno una fracción. Aldo escribió una fracción que tiene el denominador 4 unidades mayor que el  numerador . Bea escribió una fracción con numerador igual al de la fracción de Aldo y  denominador 5 unidades mayor que el denominador de la fracción de Aldo.  La fracción de Bea es equivalente a 1/2 .  ¿Cuál es la fracción que escribió Aldo?   ¿Cuál es la fracción que escribió Bea?

2 Carlos tiene dos piezas triangulares pequeñas y dos piezas triangulares grandes. Cada pieza triangular pequeña tiene 36 cm de perímetro. Cada pieza triangular grande tiene 48 cm de perímetro. Carlos arma: Con las dos piezas triangulares pequeñas,  un rectángulo de 42 cm de perímetro. Con las dos piezas triangulares grandes, un rectángulo de 56 cm de perímetro. Con las 4 piezas, el rectángulo de la figura, de 74 cm de perímetro. ¿Qué longitud tiene cada uno de los lados de las piezas triangulares?

3   Con papeles de colores rojo, verde y azul,  se quieren cubrir las franjas de este barrilete de manera que haya por lo menos una franja de cada color y que las franjas que tienen un lado en común sean de colores distintos.
 ¿De cuántas maneras puede hacerse?

Segundo Nivel

1  Miguel sube la escalera de uno en uno. Daniel baja la escalera de dos en dos. Daniel baja dos escalones en el mismo tiempo en que Miguel sube uno. Ayer, cuando Miguel había subido 11 escalones Daniel empezó a bajar. Cuando Daniel terminó de bajar, a Miguel le faltaba subir 8 escalones.  ¿Cuántos escalones tiene la escalera?

2  A, B, C, D y E representan dígitos distintos.

     Si         ABC
              +    C5
                   DE     
                  B95
¿Cuánto pueden valer A, B, C, D y E? Da todas las soluciones distintas.  ¿Cuáles dan la mayor suma?

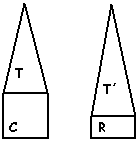
3 La figura 1 está formada por un cuadrado C y un triángulo T.   C y T tienen igual área. La figura 2 está formada por un rectángulo R y un triángulo T´. El cuadrado C y el rectángulo R tienen igual base. La altura de R es la mitad de su base. La figura 1 y la figura 2 tienen igual altura.    La suma de las áreas de las dos figuras es 135 cm2.  ¿Cuál es el área del triángulo T´?                          

Tercer Nivel

1  A = 10¹⁰⁰ – 2005             B = 10²⁰⁰⁵ - 2005  
¿Cuál es la suma de las cifras del número A? 
¿Cuál es la suma de las cifras del número B?

2    A, B, C, D, E, F, G, H, I, J, K y L son los vértices de un dodecágono regular. El triángulo ABC tiene 4,28 cm2­ de área. ¿Cuál es el área del dodecágono ABCDEFGHIJKL? 
(Un dodecágono es un polígono de 12 lados.)

3    Juan dibujó un rectángulo con lados de longitudes enteras. Trazó paralelas a los lados y el rectángulo quedó dividido en 72 cuadrados iguales    con lados de longitudes enteras. Si el área del rectángulo que dibujó Juan es menor que 2005 cm2, ¿qué dimensiones puede tener el rectángulo que dibujó Juan?  Da todas las posibilidades.

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar