XXXIX Olimpíada Internacional de Matemática
15 y 16 de Junio de 1998. Taipei, Taiwan
| primer día |
1
En el cuadrilátero convexo ABCD, las diagonales AC y BD son perpendiculares y los lados opuestos AB y DC no son paralelos. El punto P intersección de las mediatrices AB y DC está en el interior del cuadrilátero ABCD. Demuestre que los vértices de ABCD están en una misma circunferencia si y sólo si los triángulos ABP y CDP tienen áreas iguales.
2
En una competencia hay a concursantes y b
jueces, con b![]() 3 un entero impar. Cada
juez califica a cada concursante como "apto" o "no
apto". Sea k un número tal que, para cada dos
jueces sus decisiones coinciden a lo más en k
concursantes. Demuestre que
3 un entero impar. Cada
juez califica a cada concursante como "apto" o "no
apto". Sea k un número tal que, para cada dos
jueces sus decisiones coinciden a lo más en k
concursantes. Demuestre que
![]() .
.
3
Para cada entero positivo n denotamos por d(n) el número de divisores positivos de n (incluyendo 1 y n). Encuentre todos los enteros positivos k para los que existe algún n tal que
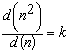
| segundo día |
4
Encuentre todas las parejas de enteros positivos (a,b) tales que a2b+a+b es divisible por ab2+b+7.
5
Sea I el centro de la circunferencia inscrita en el triángulo ABC. Esta circunferencia es tangente a los lados BC, CA y AB del triángulo en los puntos K, L y M, respectivamente. La recta paralela a MK que pasa por el punto B interseca a las rectas LM y LK en los puntos R y S, respectivamente. Demuestre que el ángulo RIS es agudo.
6
Sea N el conjunto de los enteros positivos. Se consideran todas las funciones f de N en N que satisfacen
f(t2 . f(s)) = s(f(t))2,
para todo s y t de N. Halle el menor valor posible de f(1998).
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |